Auteur: Georges Quénot.
Cette page n'est pas terminée.Nous allons considérer directement le cas d’un polygone régulier à \( m \) côtés avec \( m \geq 3 \). Le cas particulier du carré correspond à \( m = 4\).
Considérons un repère \( Oxyz \) et un cercle \( \cal{C} \) de centre \( O \) et de rayon \( h \) placé dans le plan \( Oxy \).
Considérons le polygone régulier à \( m \) côtés \( \cal{P}_m \) de centre \( O \) placé également dans le plan \( Oxy \), dont un des côtés coupe perpendiculairement la demi-droite \( Ox \) avec \( x \geq 0 \) et dont l’aire est égale à celle du cercle de rayon \( h \). Appelons \( a \) la distance du point \( O \) aux côtés du polygone. On a (par l’égalité des aires) \( a = h \sqrt{(\pi/m) / \tan (\pi/m)} \).
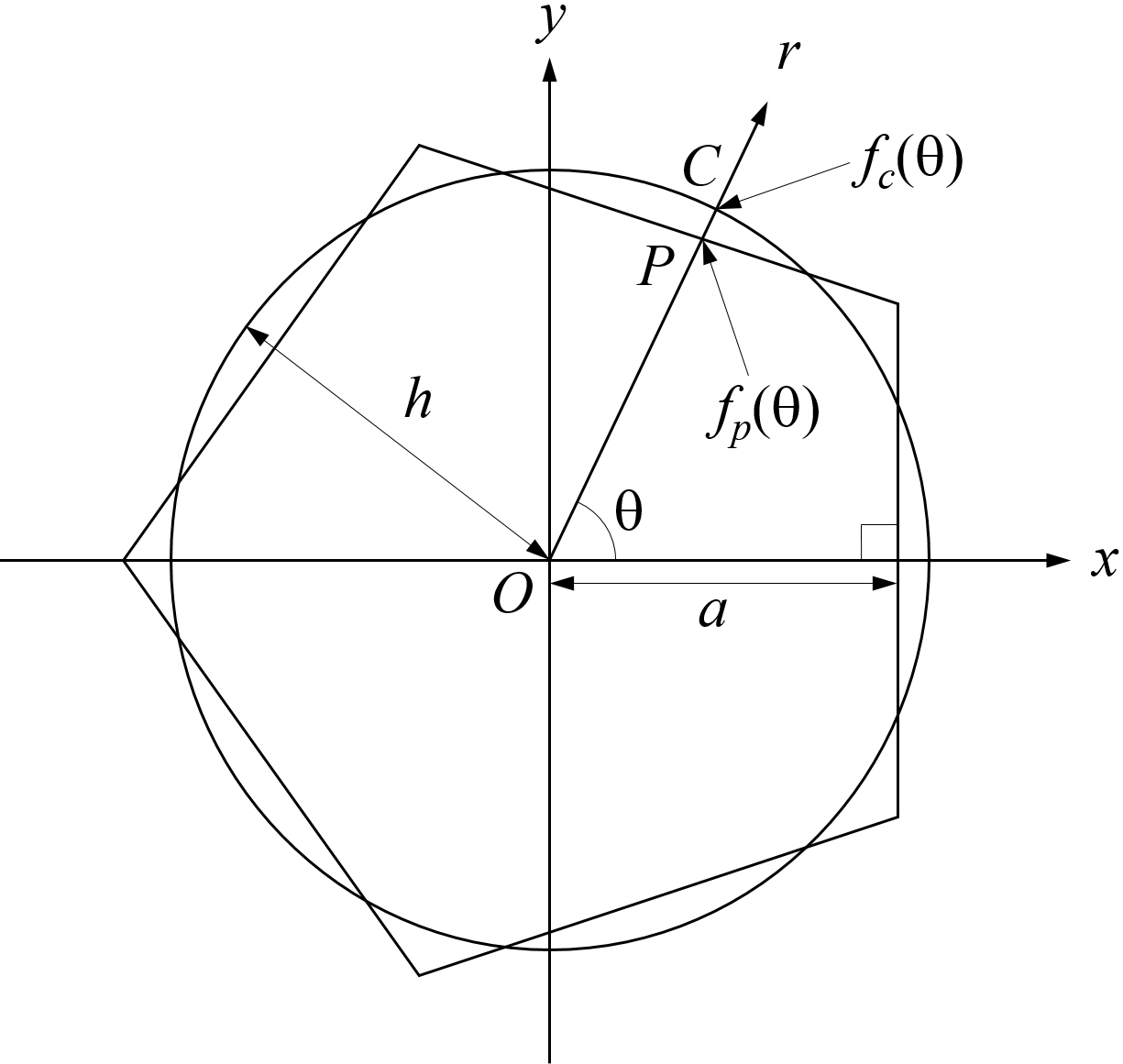
On peut utiliser une représentation paramétrique en coordonnées polaires dans le plan \( Oxy \) de type \( r = f(\theta) \) avec \( x = r \cos \theta \) et \( y = r \sin \theta \) pour décrire le cercle \( \cal{C} \) et le polygone \( \cal{P}_m \). Pour le cercle, on a simplement \( f_c(\theta) = h \). Pour le polygone, la fonction \( f_p \) est périodique de période \( 2 \pi/m \) et est définie entre \( - \pi/m \) et \( + \pi/m \) par \( f_p(\theta) = a / \cos \theta \). Considérons l’axe \( Or \) qui fait un angle \( \theta \) avec \( Ox \) dans le plan \( Oxy \). Le cercle coupe cet axe en un point \( C \) d’abscisse \( f_c(\theta) \) et le polygone coupe cet axe en un point \( P \) d’abscisse \( f_p(\theta) \). La figure 1 montre le cercle et le polygone pour \( m = 5 \) et elle illustre leur représentation paramétrique dans le plan \( Oxy \).

Considérons deux points \( A_c \) et \( A_p \) (qui seront les deux points de vue) placés sur l’axe \( Oz \) à égale distance \( d \) du plan \( Oxy \), respectivement au-dessus (abscisse \( +d \)) et au-dessous (abscisse \( -d \)) du plan \( Oxy \). Considérons le cône de sommet \( A_c \) qui passe par le cercle \( \cal{C} \) et la pyramide à \( m \) faces de sommet \( A_p \) qui passe par le polygone \( \cal{P}_m \). Le cône est constitué de l’ensemble des demi-droites issues de \( A_c \) et passant par les points du cercle. La pyramide est constituée de l’ensemble des demi-droites issues de \( A_p \) et passant par les points du polygone.
Considérons, pour chaque angle \( \theta \), le demi-plan \( Ozr \) avec \( r \geq 0 \) passant par les axes \( Oz \) (fixe) et \( Or \) (correspondant à l’axe \( Ox \) tourné de l’angle \( \theta \) autour de \( Oz \)). Une et une seule demi-droite du cône se trouve dans ce demi-plan et elle coupe le plan \( Oxy \) au point \( C \) et une et une seule demi-droite de la pyramide se trouve dans ce demi-plan et elle coupe le plan \( Oxy \) au point \( P \) (comme dans la figure 1). Ces deux demi-droites, \( [A_c C) \) et \( [A_p P) \), se coupent en un point \( M \). Le lieu de ces points sur l’ensemble des valeurs possible de l’angle \( \theta \) est une courbe qui est l’intersection du cône et de la pyramide. Cette courbe est vue comme le cercle \( \cal{C} \) depuis le point \( A_c \) et comme le le polygone \( \cal{P}_m \) depuis le point \( A_p \) puisque, pour chaque valeur de \( \theta \), \( A_c \), \( C \) et \( M \) sont alignés (\( M \) est vu comme \( C \) depuis \( A_c \)) et \( A_p \), \( P \) et \( M \) sont alignés (\( M \) est vu comme \( P \) depuis \( A_p \)). La figure 2 illustre l’intersection du cône et de la pyramide dans le demi-plan \( Ozr \).
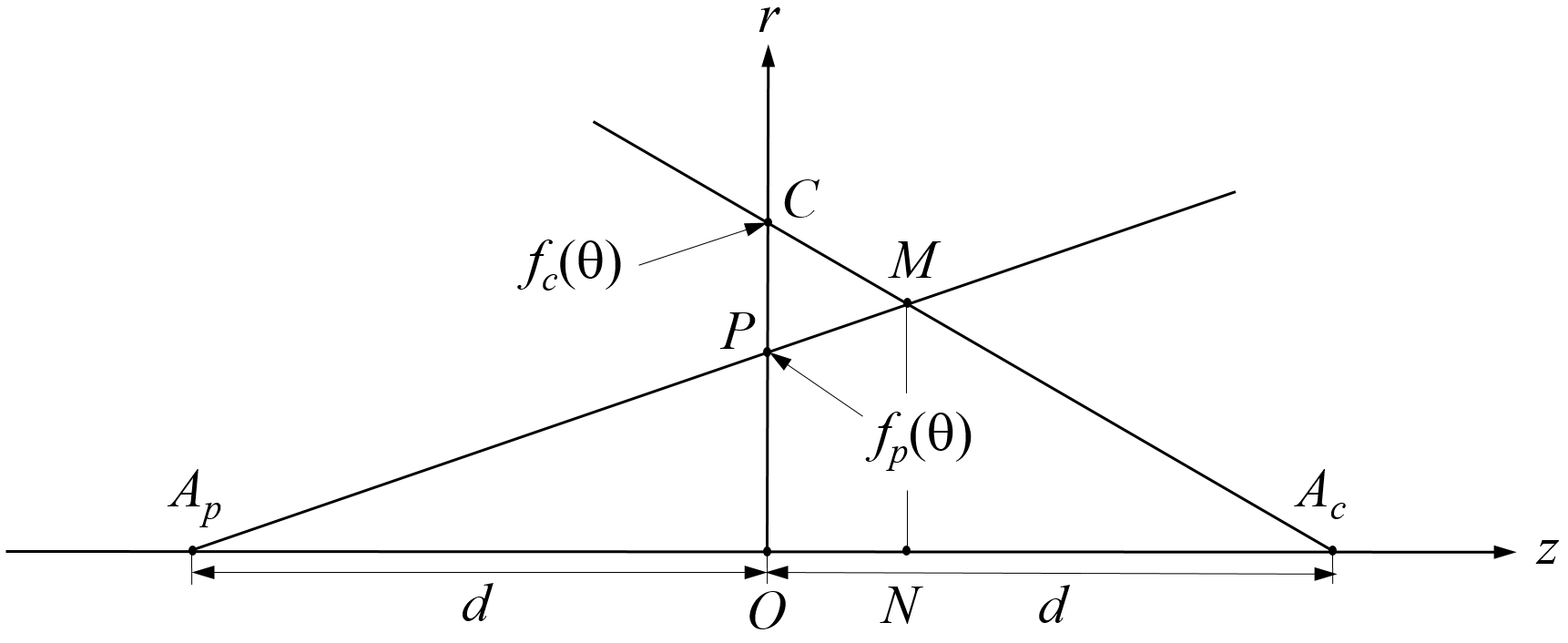
Les notations ont jusqu’ici été simplifiées et les points \( C \), \( P \) et \( M \) doivent normalement être notés \( C(\theta) \), \( P(\theta) \) et \( M(\theta) \). Dans la représentation paramétrique selon la variable \( \theta \), leurs coordonnées cylindriques \( (r,\theta,z) \) sont respectivement \( (h,\theta,0) \), \( (f_p(\theta),\theta,0) \) et \( (f_r(\theta),\theta,f_z(\theta)) \), \( f_z(\theta) \) et \( f_r(\theta) \) étant les coordonnées du point \( M \) dans le demi-plan \( Ozr \). Appelons \( N \) la projection du point \( M \) sur l'axe \( Oz \). Les triangles \( P A_p O \) et \( M A_p N \) d'une part et les triangles \( C A_c O \) et \( M A_c N \) d'autres part sont semblables. On en déduit assez facilement (2 équations à 2 inconnues) : \[ f_r(\theta) = h \; \frac{2}{h/f_p(\theta)+1} \] \[ f_z(\theta) = d \; \frac{h/f_p(\theta)-1}{h/f_p(\theta)+1} \] Notons que \( h/f_p(\theta) \) ne dépend en fait pas de \( h \) car, comme indiqué précédemment, la fonction \( f_p \) est périodique de période \( 2 \pi/m \) et est définie entre \( - \pi/m \) et \( + \pi/m \) par \( f_p(\theta) = a / \cos \theta \) avec \( a = h \sqrt{(\pi/m) / \tan (\pi/m)} \). Si on note \( c_m \) la constante \( \sqrt{\tan (\pi/m) / (\pi/m)} \), on obtient, pour \( \theta \) entre \( - \pi/m \) et \( + \pi/m \) : \[ f_r(\theta) = h \; \frac{2}{c_m \cos \theta+1} \] \[ f_z(\theta) = d \; \frac{c_m \cos \theta-1}{c_m \cos \theta+1} \] soit, en coordonnées cartésiennes, toujours pour \( \theta \) entre \( - \pi/m \) et \( + \pi/m \) : \[ f_x(\theta) = h \; \frac{2 \cos \theta}{c_m \cos \theta+1} \] \[ f_y(\theta) = h \; \frac{2 \sin \theta}{c_m \cos \theta+1} \] \[ f_z(\theta) = d \; \frac{c_m \cos \theta-1}{c_m \cos \theta+1} \] et finalement, pour \( \theta \) entre \((2k-1)\pi/m \) et \((2k+1)\pi/m \) (quel que soit l’entier \( k \)) : \[ f_x(\theta) = h \; \frac{2 \cos \theta}{c_m \cos (\theta-2k\pi/m)+1} \] \[ f_y(\theta) = h \; \frac{2 \sin \theta}{c_m \cos (\theta-2k\pi/m)+1} \] \[ f_z(\theta) = d \; \frac{c_m \cos (\theta-2k\pi/m)-1}{c_m \cos (\theta-2k\pi/m)+1} \] On obtient la courbe “cercle polygone” complète en faisant varier \( k \) de \( 0 \) à \( m-1 \) puis \( \theta \) de \((2k-1)\pi/m \) à \((2k+1)\pi/m \). Pour chaque valeur de \( k \), on obtient une “arche” (qui est une arc d’hyperbole car \( c_m \gt 1\)) correspondant à l’intersection entre le cône et une des faces de la pyramide. On remarque que la position du point \( M \) est proportionnelle à \( h \) et ne dépend pas de \( d \) pour ses coordonnées \( x \) et \( y \) et qu’elle est proportionnelle à \( d \) et ne dépend pas de \( h \) pour sa coordonnée \( z \). À un facteur d’échelle près, la courbe ne change pas si on multiplie \( h \) et \( d \) par un même facteur. Par contre, le relief relatif (la hauteur en \( z\) de la figure par rapport à la taille du cercle) change proportionnellement au rapport \( d/h \). Le relief relatif est aussi d’autant plus important que le nombre de côtés est faible pour une même valeur de \( d/h \).
Les trois dernières équations peuvent être utilisées pour construire et visualiser informatiquement une approximation de la courbe. L'approximation consiste à remplacer chaque arche par une courbe composée de \( 2n \) segments rectilignes. Ceci est fait en décomposant chaque intervalle \( [(2k-1)\pi/m,(2k+1)\pi/m] \) en \( 2n \) parties égales. La courbe totale est composée de \( 2mn \) segments. La génération de la courbe dépend des quatre paramètres \( m \), \( h \), \( d \) et \( n \).
Les fichiers VRML ci-dessous contiennent des représentations de courbes pour des valeurs de \( m \) égales à 3, 4, 5 et 6. Les valeurs de \( h \) et \( d \) ont été choisies respectivement à 50 et 400, soit un rapport \( d/h \) de 8, ce qui correspond à un relief relatif proche de 1 pour le “cercle carré”. Les valeurs de \( n \) ont été choisies de telle sorte que chaque courbe contienne au moins 160 segments au total (\( n = 20 \) pour le cercle carré). Il vous faut un visualiseur VRML (e.g. FreeWRL) pour voir les fichiers wrl et manipuler directement les objets :
La distance à l'écran optimale pour regarder la figure est de 4 fois (\( d/2h \)) le diamètre du cercle. Cinq points de vue sont prédéfinis dans les fichiers VRML et freeWRL permet de naviguer automatiquement de l'un à l'autre (flèches en bas). Les deux premiers points de vue sont situés aux points \( A_c \) et \( A_p \) respectivement. Les trois autres sont intermédiaires entre ces deux-là lorsqu'on effectue une rotation autour de l'objet par le côté (faire tourner l'objet ou tourner autour de lui en sens opposé est équivalent). Ci-dessous, les mêmes courbes avec visualisation en plus du cercle et du polygone dans le plan \( Oxy \).
En construction
Pour effectuer une réalisation physique, il est nécessaire de donner une épaisseur à la forme. Une première possibilité est de lui donner une section circulaire en l'élargissant selon un rayon constant. On pourrait par exemple effectuer une réalisation en cintrant un tube ou un fil de fer. L'inconvénient de cette solution est que les parties les plus proches apparaîtraient plus épaisses que les parties les plus éloignées et que les deux bords extérieurs n'apparaîtraient pas comme des cercles ou des polygones réguliers parfaits. L'effet relatif décroît avec \( m \) et il n'est pas négligeable, au moins dans les cas du cercle triangle (~43%) et du cercle carré (~19%).
L'idéal est que les bords extérieurs de la forme épaissie apparaissent comme des cercles parfaits ou comme polygones réguliers des parfaits depuis chacun des points de vue, c'est à dire que la forme apparaisse comme la surface délimitée par ces deux cercles ou ces deux polygones réguliers comme montré sur la figure 3. Notons \( h^- = h (1 - \epsilon_h) \) et \( h^+ = h (1 + \epsilon_h) \) les rayons des cercles intérieurs et extérieurs rapportés au plan \( z = 0 \). Pour chacune de ces deux valeurs, il y a un cône, une pyramide et une courbe intersection associés. Pour que l'effet visuel soit optimal, il faut que \( \epsilon_h \)soit aussi petit que possible par rapport à \( 1\).

Pour chaque valeur de \( \theta \), les équations ci-dessus donnent la position de deux points \( M^- \) et \( M^+ \) dans le demi-plan \( Ozr \) correspondants aux deux valeurs \( h^- \) et \( h^+ \). La figure 4 illustre les intersections des deux cônes et des deux pyramides correspondants dans le demi-plan \( Ozr \). Comme \( f_z(\theta) \) ne dépend pas de \( h \), les points \( M^- \) et \( M^+ \) ont la même abscisse points \( z \) et le segment points \( [M^-M^+] \) est parallèle à l'axe \( Or \). Soit \( M_p \) (resp. \( M_c \)) l'intersection des demi-droites \( [A_c M^-) \) et \( [A_p M^+) \) (resp. \( [A_c M^+) \) et \( [A_p M^-) \)).
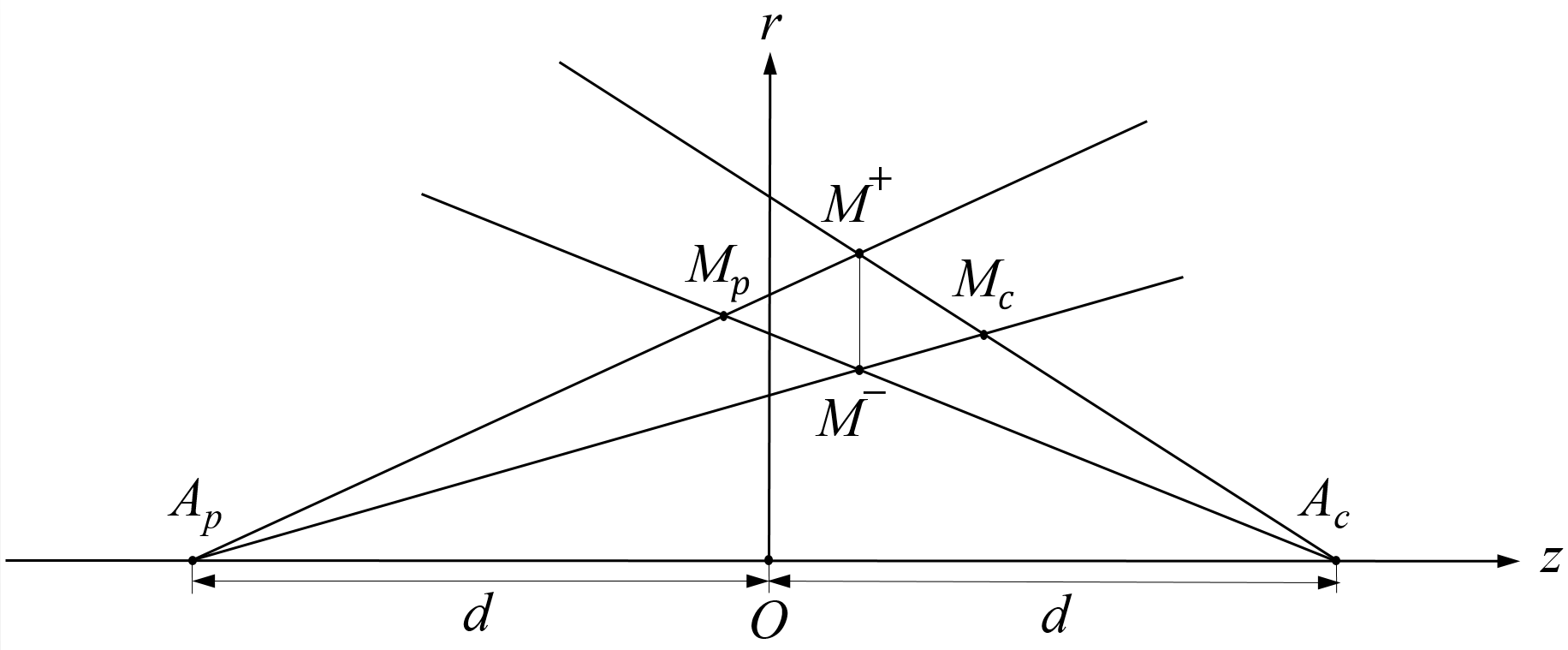
Pour que la forme apparaisse comme souhaité depuis chacun des deux points de vue, il suffit que, pour toutes les valeur de \( \theta \), la section de la forme dans le demi-plan \( Ozr \) passe par les points \( M^- \) et \( M^+ \) tout en restant à l'intérieur du quadrilatère \( M^- M_c M^+ M_p \). Une possibilité est de considérer la forme construite en prenant exactement ce quadrilatère comme section. Ceci a l'inconvenient que ce quadrilatère est en pratique très allongé dans le sens l'axe \( Oz \), \( d \) devant être choisi grand par rapport à \( h \). Une autre possibilité est de considérer la forme construite en prenant une section qui est un polygone dont \( M^- \) et \( M^+ \) sont des sommets et inclus dans la quadrilatère \( M^- M_c M^+ M_p \).
En construction.
En construction.
En construction.
En construction.
En construction.